What Perfect Square: Definition, List, Notation, Characteristics, Facts, Examples
A perfect square is a result of multiplying an integer by itself. Find the list of perfect squares from 1 to 20 here.
A Perfect Square is an interesting number that connects to many situations in practical life. Whether you are solving puzzles or identifying geometric patterns, the concept of this number helps you find solutions simply and quickly.
This article will discuss the perfect number of squares, its characteristics, and ways to identify them, along with solved examples for better understanding and applications.
What Perfect Square?
A squares is a number obtained when an integer is multiplied by itself. The perfect square is a positive integer, which is the product of the same two positive or negative integers. For example, when we multiply 6 by 6, we get 36, a perfect square number. Again, the product of (-) 8 and (-) 8 gives another perfect square, 64.
What Perfect Square
Notation of Perfect Square
The square can be represented as the square of a given number when the number is raised to the power of 2.
So, a square can be expressed as x2, where x is an integer and the value of x2 is a perfect square.
For example, a square 25, which is a product of 5 and 5, can be written as: 25 = 52
Why Perfect Square Always Positive?
A square is always positive because the product is always positive, whether we multiply two positive integers or two negative integers. This applies the following principle:
- +ve x +ve = +ve
- -ve x -ve = +ve
What Perfect Square
The Square Root Concept to Identify a Perfect Square
To determine whether a number is a square, we calculate the square root of the given number. If the result of the square root is a whole number, then the given number is a perfect square. If the square root doesn’t provide a whole number, the given number is not a perfect square.
For example, if we take the square root of a given number, say, 49, we get the result as 7, which is a whole number. Therefore, 49 is a perfect square.
Again, for a given number 60, we calculate the square root, which is approximately 7.75. Since it is not a whole number, 60 is not a perfect square.
What Perfect Square
Identify Perfect Square by Prime Factorization
Prime factorization is finding a given number’s prime factors so that when these factors are multiplied, the product is the given number. To identify a square number, we perform prime factorization and determine whether only one prime number occurs even times.
For example, if we do prime factorization of 625, we get 625 = 5 x 5 x 5 x 5.
Here, 5 is multiplied 4 times, so 625 is a square, and the square root of 625 is 5 x 5 = 25.
Characteristics of Perfect Square Numbers
The last digit, or the digit at one’s place of a number, indicates whether a number is a square. If the last digit of a number is 2, 3, 7, or 8, it cannot be a square. Perfect numbers always end with any of the digits 0, 1, 4, 5, 6, and 9.
A perfect number must have an even number of zeros at the end. For example, 400 and 900 are even numbers. But there is a deviation to it. The number 300 has even zeros, but it is not a square.
What Perfect Square
Observations Made About the Perfect Square
- The numbers that end with 3 and 7 will have 9 as the unit’s place digit in its square.
- The number ending with 5 will have 5 at the unit place in its square number.
- The number ending 4 or 6 will generate an ideal square with 6 as the unit’s place digit.
- The numbers that end with 2 or 8 will have 4 at the unit’s place digit in its square number.
- The numbers ending with 1 and 9 will generate square with 1 as a digit in the unit’s place.
What Perfect Square
A List of Perfect Squares from 1 to 10
Here is a list of squares for the numbers 1 to 10 for ready reference.
| A List of Perfect Squares from 1 to 10 | |
| Natural number | Perfect square |
| 1 | 1 × 1 = 1 |
| 2 | 2 × 2 = 4 |
| 3 | 3 × 3 = 9 |
| 4 | 4 × 4 = 16 |
| 5 | 5 × 5 = 25 |
| 6 | 6 × 6 = 36 |
| 7 | 7 × 7 = 49 |
| 8 | 8 × 8 = 64 |
| 9 | 9 × 9 = 81 |
| 10 | 10 x 10 = 100 |
Perfect Square Important Points
- A square that ends with zero will always have an even number of zeros at the end.
- Squares are always positive.
- The square roots of perfect squares may be positive or negative.
- We can also find perfect cubes by multiplying a square with its square root.
- A square has any digits 0, 1, 4, 5, 6, and 9 at its unit place.
- A square of an even number is always even.
- A square of an odd number is always odd.
- The sum of the first n odd numbers is always a perfect square.
What Perfect Square
Geometrical Correlation of a Perfect Square
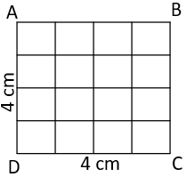
A square can be related to the area of a squared geometrical shape. A square has equal sides, so by multiplying the value of one side by the value of another side, we get the area of the square, which is a square of the dimension of its side.
For example, if all sides of a square ABCD are 4 cm, then the area of the square is 4 cm x 4 cm = 16 square cm. This value is a perfect square of 4 cm.
What Perfect Square
Trinomial Expression of Perfect Square
A square can be expressed as a trinomial expression. For example, if there are two integers a and b, we can use the following trinomial expressions to find the perfect square.
- (a + b) x (a + b) = (a + b)2= a2 +2ab+b2
- (a – b) x (a – b) = (a – b)2= a2 + 2ab + b2For
For example, let’s take the number 28. To get the square of this number, we can use the above formula.
We can write 28 = 20 + 8
So, (28)2 = (20 + 8)2 = (20)2 + 2 x 20 x 8 + (8)2 = 400 + 320 + 64 = 784
What Perfect Square
What Perfect Square Solved Examples
1. If the radius of a circle is 3 cm, find its area.
Solution:
The formula for the area of a circle is Area= 3.14r2, where r is the radius.
Here, r = 3 cm
So, the area of the circle is A = 3.14 x (3)2 = 3.14 x 9 = 28.26 square cm.
2. Is the number 196 a perfect square? Find its square root.
Solution:
By prime factorization, we get 196 = 2 x 2 x 7 x 7
So, it is a square, and its square root is 2 x 7 = 14.
3. In an assembly, there are 12 rows, and in each row, there are 12 students. Find the total number of students in the assembly.
Solution:
The number of rows is the same as the number of students in each row, which means the arrangement is square. So, the total number of students will be, (12)2 = 12 x 12 = 144.
4. What Perfect Square of the number 94.
Solution:
We will use the trinomial expression to simplify the solution.
We can write 94 = 100 – 6
So, (94)2 = (100 – 6)2 = (100)2 – 2 x 100 x 6 + (6)2 = 10000 – 1200 + 36 = 8836
What Perfect Square
Read More – Median of a Triangle: Definition, Formula, and Examples

My name is Khushi, I am a content writer and I provide news related to government jobs and I am from Rajasthan and I only write on this website.