Surface Area Formulas: Definitions, Derivations, Examples
Surface Area Formulas define how to calculate the outer surface of 3D shapes. Check out surface area formulas for various three-dimensional shapes with solved examples here.
Surface area is all about understanding the outer space covered by a 3D object. From cubes and spheres to cones and cylinders, every shape has its own unique way of measuring surface area.
But why is it important?
Whether it’s figuring out how much wrapping paper is needed for a gift box or how much paint to cover a ball, surface area helps solve everyday problems in fun and creative ways. In this blog, we will discuss the surface area formulas of different three-dimensional geometrical shapes.
What is Surface Area?
Surface area is the total outer area of a three-dimensional object, describing the space its surfaces occupy. It is used by designers, engineers, and architects to calculate materials for wrapping, painting, or construction.
Measured in square units like cm² or m², surface area has two types:
Lateral Surface Area (LSA): This measures the area of the vertical or curved sides of an object. It excludes the top and bottom faces. For example, the label around a cylindrical can represents its lateral surface area.
Total Surface Area (TSA): This includes the area of all surfaces of the object, covering the top, base, and sides. It represents the complete outer area. For instance, the entire outer covering of a box is its total surface area.
These types ensure clarity when calculating specific areas of a three-dimensional figure.
Surface Area Formulas
Surface Area Formulas are used to calculate the total surface area, which includes all surfaces (base and sides), and the lateral surface area, which covers only the sides. Below is a table of important surface area formulas for various three-dimensional figures.
| Surface Area Formulas | ||
| Shape | Lateral Surface Area (LSA) | Total Surface Area (TSA) |
| Cube | 4a2 | 6a2 |
| Cuboid | 2h(l+b) | 2(lb + lh + bh) |
| Cylinder | 2πrh | 2πr(r + h) |
| Cone | πrl | πr(l + r) |
| Sphere | 4πr2 | 4πr2 |
| Hemisphere | 2πr2 | 3πr2 |
| Pyramid | 1/2 × (Base Perimeter) × (Slant Height) | Lateral Surface Area+ Area of Base |
Surface Area of Different Geometrical Shapes
Here, we will discuss the meaning of the surface area of different three-dimensional geometrical shapes, including cubes, spheres, cylinders, cuboids, cones, and pyramid along with their formulas and examples to understand their practical applications.
Surface Area Formulas
Surface Area of Cube
The surface area of a cube is the total area covered by its six square faces. A cube is a 3D geometric shape where all sides are equal and each face is a square. The surface area of a cube is expressed in terms of square units (e.g., cm2,m2,in2)
There are two types of surface areas for a cube:
- Total Surface Area (TSA
- Lateral Surface Area (LSA)
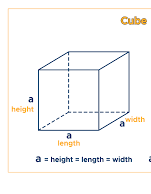
Total Surface Area (TSA) of a Cube: The total surface area of a cube is the combined area of all six square faces. Since each face is a square with equal sides, the total surface area can be calculated by summing up the areas of all six faces.
TSA of Cube Formula = 6a2
Where a is the length of one side of the cube.
Lateral Surface Area (LSA) of a Cube: The lateral surface area of a cube refers to the total area of its four vertical faces, excluding the top and bottom faces. Each lateral face is a square, and since there are four of them, the lateral surface area is four times the area of one square face.
LSA of Cube Formula = 4a2
Where a is the side length of the cube.
Surface Area Formulas
Surface Area of Cube Example
Find the total and lateral surface area of a cube with a side length of 8 cm.
Solution:
Given Data:
Side of the cube (a) = 8 cm
Step 1: Total Surface Area (TSA)
The formula for the total surface area of a cube is:
TSA=6a2
Substitute the given side length:
TSA=6×(8)2 =6×64=384 cm2
Step 2: Lateral Surface Area (LSA)
The formula for the lateral surface area of a cube is:
LSA=4a2
Substitute the given side length:
LSA=4×(8)2 = 4×64=256 cm2
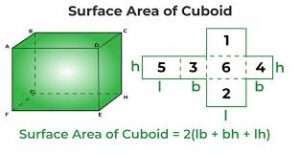
Surface Area of Cuboid
The surface area of a cuboid refers to the total area covered by all of its surfaces. Since a cuboid is a 3D form of a rectangle, its surface area depends on its length, breadth, and height.
A cuboid has two main types of surface areas. They are:
- Total surface area of a cuboid
- Lateral surface area of a cuboid
Total Surface Area (TSA): The total surface area of a cuboid is the sum of the areas of all six rectangular faces. Since opposite faces are equal, it can be calculated as:
TSA of Cuboid Formula:=2(lb+bh+lh) square units
Where l is the length, b is the breadth, and h is the height of the cuboid.
Lateral Surface Area (LSA): The lateral surface area refers to the area of the four vertical faces, excluding the top and bottom faces. It is calculated as:
LSA of Cuboid Formula: = 2h(l+b) square units
Surface Area of Cuboid Examples
Example 1: Determine the lateral surface area of a cuboid with the following dimensions:
- Length (l) = 18 in
- Breadth (b) = 10 in
- Height (h) = 14 in
Surface Area Formulas
Solution:
We know the formula for the lateral surface area of a cuboid:
LSA=2h(l+b)
Step 1: Substitute the given values into the formula:
LSA=2×14×(18+10)
Step 2: Simplify:
LSA=2×14×28 =2×392=784 square inches
Surface Area of a Sphere
The surface area of a sphere represents the total area occupied by its surface.
Example:
Find the surface area of a sphere with a radius of 7 cm.
The formula is Surface Area of Sphere is =4πr2
Substituting r=7
Surface Area=4×3.14×72=615.4 cm2
Thus, the surface area of the sphere is 615.4 cm².
Surface Area Formulas
Curved Surface Area (CSA) of a Sphere
Since the sphere has only one curved surface, the curved surface area equals the total surface area:
CSA=4πr2
Total Surface Area (TSA) of a Sphere
The TSA is the same as the CSA, as the entire sphere is curved:
TSA=CSA=4πr2
Surface Area of Hemisphere
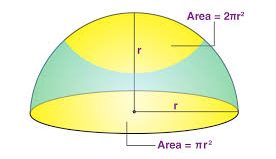
The surface area of a hemisphere refers to the total area covered by its surfaces. A hemisphere can be either solid or hollow, and its surface area is calculated in two parts:
Curved Surface Area (CSA): This is the area of the dome-shaped, curved portion of the hemisphere. It is half the total surface area of a full sphere because a hemisphere is half of a sphere.
Curved Surface Area Formula:=2πr2
Where:
R is the radius of the hemisphere.
π is a constant with a value approximately equal to 3.14.
Base Area of Hemisphere:
The base of the hemisphere is a flat circular surface. Its area is equal to the area of a circle.
Base Area of Hemisphere Formula: =πr2
Total Surface Area (TSA): The total surface area of a hemisphere includes both the curved surface area and the flat circular base. It is the sum of the curved surface area and the base area.
TSA of Hemisphere Formula:=CSA+Base Area
Substituting the formulas:
TSA of Hemisphere=2πr2+πr2=3πr2
Surface Area Formulas
Surface Area of a Hemisphere Example
Find the curved surface area (CSA) and total surface area (TSA) of a hemisphere with a radius of 5 m.
Solution:
Given:
r=5 m (radius)
Step 1: Curved Surface Area (CSA)
The formula for the curved surface area is:
CSA=2πr2
Substitute the values:
CSA=2×3.14×52
Simplify:
CSA=2×3.14×25=157 sq.
Step 2: Total Surface Area (TSA)
The formula for the total surface area is:
TSA=3πr2
Substitute the values:
TSA=3×3.14×52
Simplify:
TSA=3×3.14×25=235.5 sq. m
Surface Area Formulas
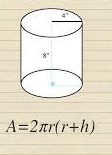
Surface Area of Cylinder
The surface area of a cylinder is the total area of its outer surface, which includes the curved (side) surface and the areas of its two circular bases. Imagine a cylinder-shaped object, like a can of soda.
To calculate the surface area of this cylinder, it can be divided into two parts:
Curved Surface Area (CSA): This is the area of the curved side of the cylinder. Think of unrolling the curved side into a rectangle. The width of this rectangle is the height (h) of the cylinder, and the length is the circumference of the circular base (2πr2).
Curved Surface Area Formula: 2πrh
Total Surface Area (TSA): The total surface area is the sum of the curved surface area and the areas of the two circular bases. Each base has an area of πr2 ,and there are two bases.
Total Surface Area Formula: 2πr2+2πrh=2πr(r+h)
Surface Area of a Cylinder Example
Find the total and lateral surface area of a cylinder with a radius of 14 cm and a height of 28 cm.
Solution:
Given:
- r= cm (radius)
- h=28 cm (height)
Surface Area Formulas
Step 1: Lateral Surface Area (LSA)
The formula for lateral surface area is:
LSA=2πrh
Substitute the values:
LSA=2×22/7×14×28
Simplify:
LSA=2×22×2×28=2464 sq. cm
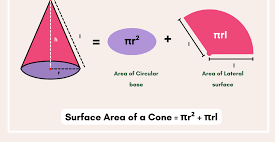
Surface Area of a Cone
The surface area of a cone is the total area covered by its boundary, which includes the curved surface area (CSA) and the total surface area (TSA).
Curved Surface Area (CSA): The CSA refers to the area of the cone’s curved surface, excluding the base. It is also called the lateral surface area.
CSA=πrl
Where r is the radius of the base, and l is the slant height of the cone.
Total Surface Area (TSA): The TSA represents the combined area of the curved surface and the circular base.
TSA=πrl+πr2
Here, is the radius of the base, and l is the slant height.
Surface Area Formulas
Find the total surface area and curved surface area of a cone if its radius is 12 cm and its slant height is 16 cm. (Use π=3.14)
Solution:
Given:
- Radius of cone (r) = 12 cm
- Slant height (l) = 16 cm
Step 1: Curved Surface Area (CSA)
The formula for the curved surface area of a cone is:
CSA=πrl
Substitute the values:
CSA=3.14×12×16
Simplify:
CSA=602.88 sq. cm
Step 2: Total Surface Area (TSA)
The formula for the total surface area of a cone is:
TSA=πr(r+l)
Substitute the values:
TSA=3.14×12×(12+16)
Simplify:
TSA=3.14×12×28
TSA=3.14×336=1,055.04 sq. cm.
Surface Area Formulas
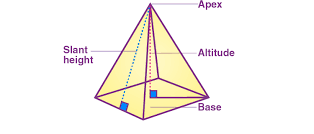
Surface Area of a Pyramid
The surface area of a pyramid is the total area covering its outer surface, including the areas of its triangular side faces (lateral surfaces) and the base. The formulas differ depending on the type of pyramid, but the general process remains the same.
Lateral Surface Area (LSA): The sum of the areas of the triangular side faces.
Lateral Surface Area Formula:=1/2×Perimeter of Base (P)×Slant Height (l) square units
Total Surface Area (TSA): The sum of the lateral surface area and the area of the base.
Total Surface Area Formula: =LSA+Area of Base square units
Surface Area Formulas for Specific Pyramids
The following table summarizes the lateral surface area (LSA) and total surface area (TSA) formulas for different types of pyramids. It also includes the key parameters needed for each calculation.
Surface Area Formulas
| Pyramid Type | Lateral Surface Area (LSA) | Total Surface Area (TSA) | Key Parameters |
|---|---|---|---|
| Triangular Pyramid | 1/2×P×l | 1/2×P×l+1/2×b×h | P: Perimeter of the triangular base b: Base of the triangle h: Height of the trianglel: Slant height of pyramid |
| Square Pyramid | 2al | 2al+a2 | a: Side length of the square base l: Slant height of pyramid |
| Rectangular Pyramid | Sum of areas of all triangular faces | LSA+l×w | l: Length of the rectangular base w: Width of the rectangular base |
| Pentagonal Pyramid | 5/2×s×l | 5/2×s×l+5/2×a×s | s: Side length of the pyramid a: Apothem length of the pentagonal base l: Slant height of the pyramid |
| Hexagonal Pyramid | 3s×l | 3s×l+3√3/2 s2 | s: Side length of the hexagonal base l: Slant height of the pyramid |
Surface Area of a Pyramid Example
A pyramid has a triangular base, where every face is an equilateral triangle. Determine the total surface area of the triangular pyramid if the side length of the base is 18 cm.
Surface Area Formulas
Solution:
Side of the base (a) = 18 cm
Step 1: Area of the Base
The formula for the area of an equilateral triangle is:
Area of Base=√3/4×a2
Substitute a=18
Area of Base=√3/4×(18)2 = √3/4× ×324≈140.05 cm2
Step 2: Area of Each Lateral Face
The lateral faces are also equilateral triangles with the same dimensions. The area of one face is the same as the base:
Area of Each Lateral Face= 140.05 cm2
Step 3: Total Surface Area (TSA)
The total surface area is the sum of the base area and the areas of the three lateral faces:
TSA= Area of Base + 3 ×Area of Each Lateral Face
TSA = 140.05 + 3 × 140.05 = 140.05 + 420.15 = 560.2
Surface Area Formulas
Read Also – What is Value of Pi in Maths: Definition, How To Calculate, Examples
My name is Khushi, I am a content writer and I provide news related to government jobs and I am from Rajasthan and I only write on this website.