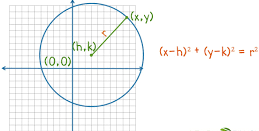Radius of a Circle: Definition, Formula, How to Find, and Examples

Radius of a Circle: Definition, Formula, How to Find, and Examples

What is Radius?

The radius is the distance from the center of a circle or sphere to its outer edge. It is an important measurement for shapes like circles, spheres, cones with circular bases, and cylinders with circular ends.

In a circle, the radius is the constant distance between the center and any point on its boundary. A circle is made up of all points that are the same distance from its center, and this distance is called the radius.

Radius Definition

The radius is the fixed distance from the center of a circle to any point on its boundary, known as the circumference.

It remains constant for a given circle and is equal to half the length of the diameter.

Represented by the symbol ‘r’, the plural form of radius is “radii.”

For example, in the figure below, points A, and B, lie on the boundary of the circle. These two points are equidistant from the center O.

As a result, the line segments OA and OB are called the radii of the circle.

Their lengths are equal, so OA = OB

How to Find the Radius of a Circle?

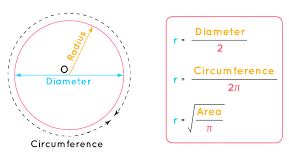
The radius of a circle can be calculated using three main formulas based on the given parameters: diameter, circumference, or area. Let’s now learn to find the area of a circle using different formulas:

If the Diameter of a circle is known

The diameter is a straight line that passes through the center of the circle, connecting two points on its boundary.

It is twice the length of the radius, making the radius half the diameter.

This relationship is expressed as:

Radius = Diameter/2​

For example, if the diameter of a circle is 10 units, the radius will be 10÷2 = 5 units.

If the Circumference of a circle is known

The circumference is the perimeter of a circle, representing the distance around it. The relationship between the radius and circumference is given by:

C=2πr

Here, C is the circumference, r is the radius, and π is approximately 3.14159. Rearranging the formula to find the radius:

Radius = Circumference/2π

For example, if the circumference of a circle is 31.4 units, the radius can be calculated as:

Radius = 31.4/2π≈5 units.

If the area of a circle is known

The area of a circle represents the space it covers and is related to the radius by the formula:

A=πr2

Where A is the area and r is the radius. To find the radius from the area:

Radius = Area/π

For example, if the area of a circle is 78.5 square units, the radius can be calculated as:

Radius = 78.5/π ≈5 units.

Radius Formula 

Radius Formula
Radius of a circle formula when circumference is given	C ⁄ 2π
Radius of a circle formula when diameter	d ⁄ 2
Radius of a circle formula when area is ivgen	√(A ⁄ π)

Radius of a Sphere

A sphere is a three-dimensional solid shape, and its radius is the distance from the center to any point on its surface. The radius of a sphere can be calculated using the given volume or surface area.

When the volume of a sphere is given:

The volume of a sphere measures the total space enclosed within it. When volume is given, the radius of a sphere is calculated using the following formula:

R=³√{(3V) / 4π} units

Where:

• V is the volume.
• R is the radius of the sphere, and
• π is a mathematical constant approximately equal to 3.14

When the surface area of a sphere is given:
The surface area of a sphere is the total area of its outer surface. When surface area is given, the radius of a sphere is calculated using the following formula:

R = √(A / 4π) units

Here,

• R is the radius of a sphere.
• A is the surface area of a sphere, and
• π is a mathematical constant approximately equal to 3.14

Radius of a Circle Equation

The equation of a circle on a Cartesian plane with center (h,k) is:

(x−h)²+(y−k)²= r²

Where (x,y), and r is the radius.

If the center of the circle is at the origin (0,0), the equation simplifies to:

x²+ y²= r²

The radius is then given by r =  x²+ y²

Relation Between Radius and Diameter of Circle

The radius and diameter of a circle are directly related. The diameter is twice the length of the radius, as it spans the entire circle through its center.

Mathematically, Diameter = 2 × Radius, or Radius = Diameter/2​.

This relationship helps calculate one when the other is known.

Radius of a Circle Solved Examples

Example 1: Calculate the radius of a circle with a diameter of 22 cm.

Solution:

Given,

Diameter of the circle, d = 22 cm

Using the formula:

Radius=Diameter/2

Radius=22/2 cm=11 cm

Hence, the radius of the circle is 11 cm.

Example 2: Calculate the radius of a circle with a circumference of 20 cm.

Solution:

The formula for radius using circumference is:

Radius =Circumference/2π

Given,

Circumference, C=20 cm, π=22/7

r=20/2πr

r=20×7/2×22

r=140/44

r=3.18 cm

Thus, the radius is 3.18 cm.

Example 3: Find the area and circumference of a circle with a radius of 16 cm.

Solution:

Given,
Radius, r=16 cm and π=3.14

Area of the Circle:
A=πr2
A = 3.14×(16)2
A = 3.14×256
A = 803.84 cm2

Circumference of the Circle:
C=2πr
C=2×3.14×16
C=100.48 cm

Therefore, the area is 803.84 cm2and the circumference is 100.48 cm

Example 4: Find the diameter of a circle if the area equals twice its circumference.

Solution:

Given,
Area of Circle = 2×Circumference

We know:

Area=πr²

Circumference=2πr

Substitute:

πr²=2×2πr

r² =4r

r=4 units

Now,

Diameter=2×Radius

Diameter = 2 × 4 = 8 units

Thus, the diameter of the circle is 8 units.

Reference 

Also Read : RPF Constable Application Status 2024-2025 OUT: Check Now