Linear Equation: Definition, Formula, Graph, Standard Forms, Examples

Linear Equation: Definition, Formula, Graph, Standard Forms, Examples

A linear equation is an equation that forms a straight line when graphed. Learn different formulas of linear equations along with their graphical representation here.

The Linear Equation is an interesting concept in mathematics. A linear equation can represent any straight line drawn on a plane. It provides a simple way to calculate the value of unknown variables that we often need to solve in real-life scenarios.

This article gives a detailed overview of linear equations, their various forms, formulas, graphical representations, and examples to clarify the concepts and applications.

What is a Linear Equation?

In Algebra, a mathematical expression involving variables and constants representing an equality statement is called an equation. An equation in which the highest power of the variable is always one is called a linear equation.

A linear equation can be written as ax + b = 0 or ax + by + c = 0 where a, b, and c are constants and x and y are variables with a power of one.

How to Identify Linear Equations?

In linear equations, the highest power or exponent of any of the variables is nothing other than one. So, by looking at the exponent of the variables, you can identify whether it is a linear equation. The table below explains how to distinguish between linear and nonlinear equations.

Linear Equations Identification
Equations	Linear or Nonlinear	Explanation
y = 5x – 3	Linear	The power of variables x and y are 1
x = y2 – 24	Non-Linear	The power of the variable y is 2
y + 20 = 35	Linear	The power variable y is 1
√y + 9x = 54	Non-Linear	the power of the variable y is 1/2
x – 8y +21 = 0	Linear	The power of variables x and y are 1

Linear Equation Formulas

A linear equation represents a straight line on a graph and has a maximum degree of 1 for all variables.

The formula of a linear equation can be expressed in different ways based on its form. Let’s break it down:

Slope-Intercept Form

The slope-intercept form of a linear equation is:

y=mx+c

Where:

• m = slope (how steep the line is)
• c= y-intercept (where the line crosses the y-axis)

Example:
If the equation is y=2x+3y 

• The slope (m) is 2, meaning the line rises 2 units for every 1 unit it moves right.
• The y-intercept (c) is 3, meaning the line crosses the y-axis at (0,3).

Point-Slope Form

The point-slope form of a linear equation is:

y−y₁=m(x−x₁)

Where:

• (x₁y₁) is a point on the line
• m is the slope

Example:
If the slope (m) is 4, and the line passes through the point (1,2):

y−2=4(x−1)

Simplify:

y=4x−4+2or y=4x−2y

Slope Formula

The slope of a line is how much it rises or falls compared to how far it moves horizontally.

The formula to find the slope is:

m=y₂−y₁/x₂−x₁​​

Where:

(x₁,y₁) and (x₂,y₂) are two points on the line.

Example:
If two points on the line are (1,2) and (3,6)

m=6−2/ 3−1=4/ 2=2

So, the slope is 2.

Linear Equation Standard Form

A linear equation formula is an algebraic expression that represents a linear equation. It is also called a one-degree equation.

The standard form of a linear equation is Ax + B = 0 with one variable x.

The standard form of a linear equation with two variables is Px + Qy = R.

In these equations, x and y are variables, and A, P, and Q are coefficients. B and R are called constants.

For example,

3x + 27 = 0 is a linear equation with one variable, where 3 is the coefficient of variable x and 27 is a constant.

5x + 12y = 46 is a linear equation with two variables where 5 is the coefficient of x, 12 is the coefficient of y, and 46 is a constant.

Graphical Representation of a Linear Equation

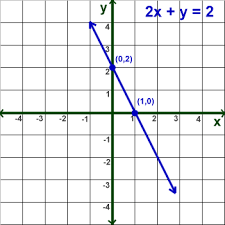
The graphical representation of a linear equation is always a straight line. Let’s take the equation 2x + y = 2.

For different values of x, we get different values of y that satisfy this expression.

When x = 0, y = 2

When x = 1, y = 0

We get a straight line by plotting the coordinates of x and y for different values and then joining the points.

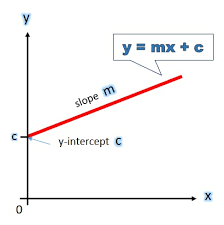
Slope- Intercept Form of Linear Equation

It is a way of expressing a linear equation in the form y = mx + c, where m is called the slope and c is the y-intercept.

For example, in the linear equation y = 2x + 13, 2 is the slope and 13 is the y-intercept.

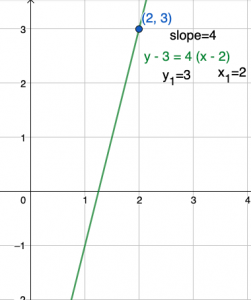
Point-Slope Form of Linear Equation

It is a way of expressing an equation when the graph of the equation passes through a point (x₁, y₁). The equation is expressed in the form: y − y₁ = m (x − x₁)

The above image shows the graph of the equation y -3 = 4(x -2). The graph passes through the point (x=2, y=3). Here, x1 = 2 and y1 = 3.

Solving Linear Equations

Solving a linear equation means finding the variable’s value or variables that satisfy the equations. The value of the variable that makes the linear equation true is called the solution of the equation.

Solving Linear Equation with One Variable

Let’s take the equation 4x – 9 = 15

To solve the equation, we bring the term with variable x to the LHS and keep the constant terms on the RHS.

Then, we calculate the value of x by dividing both sides by the coefficient of x.

4x – 9 =15

Or, 4x = 15 + 9

Or, 4x = 24

Or, x =24/4 = 6

So, the solution of the equation 4x – 9 = 15 is x = 6.

Solving Linear Equation with Two Variables

Solving linear equations with two variables means finding the values of the two variables that satisfy both equations simultaneously. The solution of linear equations with two variables involves the following steps:

• Arrange the equations in the standard form: ax+by+c=0
• Check if adding or subtracting the equations would result in the cancellation of a variable.
• If not, multiply one or both equations by either of the coefficients of x or y so that their addition or subtraction would cancel any of the variables.
• An equation with a single variable will be obtained.
• Solve the equation for the single variable.
• Put the value of this variable in any of the given equations to get the value of another variable.

Let’s take the equations 5x + 3y – 19 = 0 and 2x + 7y – 25 = 0

The addition or subtraction of these equations doesn’t cancel any variable. So, we will multiply the first equation by 2 and the second by 5. Now we get the set of two equations as follows:

10x + 6y – 38 = 0

10x + 35y – 125 = 0

By subtracting these two equations, we get:

10x + 6y – 38 – (10x +35y -125) = 0

Or, 6y -35y -38 + 125 = 0

Or, -29y = -87

Or, y = 3

Substituting the value of y in the first equation, we get:

Or, 5x + 9 -19 = 0

Or, 5x = 10

Or, x =2

Answer: The solution is: x = 2 and y =3

Linear Equations Solved Examples

1. Three times a number when added to 21, the result is 60. Find the number.

Solution:

Let the unknown number be x. Three times this number is 3x.

When added to 21, this number gives the expression 3x + 6, which equals 60.

So, we can write the linear equation, 3x + 21 = 60.

This linear equation can be solved by finding the value of x, the unknown number.

3x + 21 = 60

Or, 3x = 60 -21 = 39

Or, x = 13

Answer: The number is 13.

2. Riya is 5 years older than Rina. If the sum of their ages is 23, find their ages.

Solution:

Let Rina’s age be x years. Then, the age of Riya will be x + 5 years.

The sum of their ages is 23, which gives the linear equation x + (x+5) = 23

Let’s solve this equation for x.

x + (x + 5) = 23

or, 2x + 5 = 23

or, 2x = 18

or, x = 9

So, Rina’s age is 9 years. The age of Riya is 9 + 5 = 14 years.

Answer: Rina’s age is 5, and Riya’s age is 14. 

Read Also – How to Calculate Antilogarithms Using an Antilog Table with Examples

Reference