How to Calculate Antilogarithms Using an Antilog Table with Examples

How to Calculate Antilogarithms Using an Antilog Table with Examples

How to Calculate Antilogarithms: Antilogarithms are the reverse of logarithms. Learn steps to calculate the antilog of a number using an antilog table in this blog.

How to Calculate Antilogarithms

How to Calculate Antilogarithms Using Antilog Formula?

Before calculating the antilog of a number, it’s important to understand the two components of a logarithmic value: the mantissa and the characteristics. These parts are fundamental to the process.

The mantissa is the decimal (fractional) part of the logarithm. It represents the fine detail of the logarithmic value and is always positive, regardless of whether the logarithm itself is positive or negative.

For example:

• In log⁡(500)=2.698, the mantissa is 0.698.
• In log⁡(1000)=3.0, the mantissa is 0.
• In log⁡(0.01)=−2.0, the mantissa is 0.

The characteristic, on the other hand, is the integer part of the logarithm. It represents the magnitude or order of the number relative to powers of 10.

It can be positive or negative, depending on the number’s size.

How to Calculate Antilogarithms

For numbers greater than 1, the characteristic is determined by counting the digits to the left of the decimal point, minus one.

Example 1: log⁡(500)=2.698. The characteristic is 2 because there are 3 digits to the left of the decimal in 500, and 3−1=2.

Example 2: log⁡(1000)=3.0. The characteristic is 3 because there are 4 digits to the left of the decimal in 1000, and 4−1=3.

How to Calculate Antilogarithms

For numbers less than 1, the characteristic is calculated by counting the zeros immediately following the decimal point, negating this count, and subtracting one.

Example 1: log⁡(0.01)=−2.0. The characteristic is −2 because there is 1 zero after the decimal in 0.01, and −(1+1)=−2.

Example 2: log⁡(0.001)=−3.0. The characteristic is −3 because there are 2 zeros after the decimal in 0.001, and −(2+1)=−3

Together, the characteristic and the mantissa provide the complete logarithmic value.

To calculate the antilogarithm (inverse logarithm) of a number, you need to separate the logarithm into its characteristic (integer part) and mantissa (fractional part). The antilogarithm is then calculated using the formula:

x= 10^log⁡(x)= 10^{Characteristic+Mantissa}

How to Calculate Antilogarithms

Let’s take an example to clearly explain this process.

Example 1: Find antilog (2.4567)

Step 1: Break the logarithmic value into the characteristic and mantissa

• Given log⁡(x)=2.4567
• Characteristic = 2 (the integer part).
• Mantissa = 0.4567 (the fractional part).

Step 2: Use the antilogarithm formula

The antilogarithm can be expressed as:

x=10^log⁡(x)=10^{Characteristic+Mantissa} 

Which we rewrite as:

x= 10^{Characteristic} × 10^Mantissa

Substitute the values:

x=10²×10^0.4567

Step 3: Calculate each term

• 10²=100
• 10^0.4567= 2.8622

Step 4: Multiply the results

Now combine the results:

x=100 × 2.8622=301.6 

The antilogarithm of 2.4567 is approximately 286.22.

How to Calculate Antilogarithms

Example 2: Find antilog (4.5234) 

Solution:

To calculate the antilogarithm of 4.5234 using the antilog formula, follow these steps:

Recall the antilog formula:

antilog(x)=10^x 

Given logarithmic value:

x= 4.5234

How to Calculate Antilogarithms

Break x into the characteristic and mantissa:

Characteristic = 4 (integer part).

Mantissa = 0.5234 (decimal part).

Using the formula, rewrite x = 4.5234 as:

10^4.5234=10⁴×10^0.5234

Calculate 10⁴:

10⁴=10000

Calculate 10^0.5234
Use a scientific calculator or exponential function to compute 10^0.5234

10^0.5234≈3.34210

Multiply the results:

10⁴×10^0.5234 =10000×3.342=33420

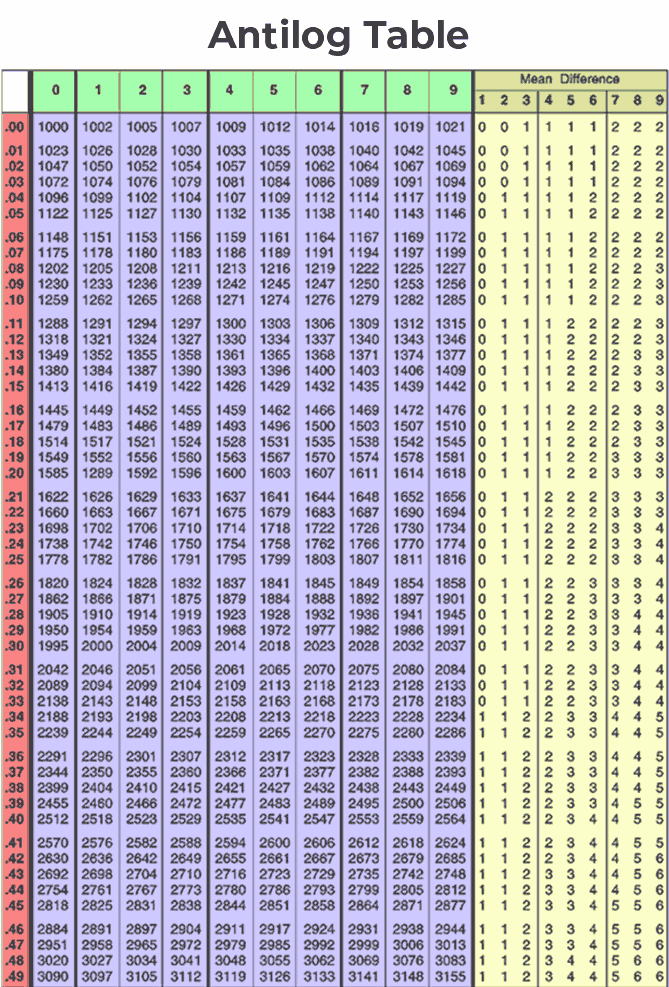
Steps to Calculate Antilog Using an Antilog Table

To calculate the antilog of a given logarithm using an antilog table, the process involves breaking the value into its characteristic and mantissa parts.

Let’s go step by step to find the antilog of 2.6452 using an antilog table:

Example 1: Calculate the antilog of 2.6452

Step 1: Separate the characteristic and mantissa

The given logarithmic value is 2.6452

• Characteristic = 2 (integer part).
• Mantissa = 0.6452 (decimal part).

How to Calculate Antilogarithms

Step 2: Use the antilog table for the mantissa

Refer to the antilog table:

1. Look for the row 0.64, which represents the first two decimal places of the mantissa.
2. Then locate column 5, which corresponds to the third digit of the mantissa (0.645).
3. The value found at row 0.640, column 5, is 4416.

Step 3: Use the mean difference for the fourth digit

• The fourth digit of the mantissa is 2.
• Using the mean difference columns in the same row, 0.64, find the value for column 2.
• The value corresponding to this is 2.

How to Calculate Antilogarithms

Step 4: Add the values from steps 2 and 3

4416+2=4418

Step 5: Insert the decimal point

• To determine the decimal point’s position, add 1 to the characteristic (2+1=3).
• This means the decimal point will be placed after the third digit from the left in 4418

Result: 4418→441.8

The antilogarithm of 2.6452 is approximately 441.8.

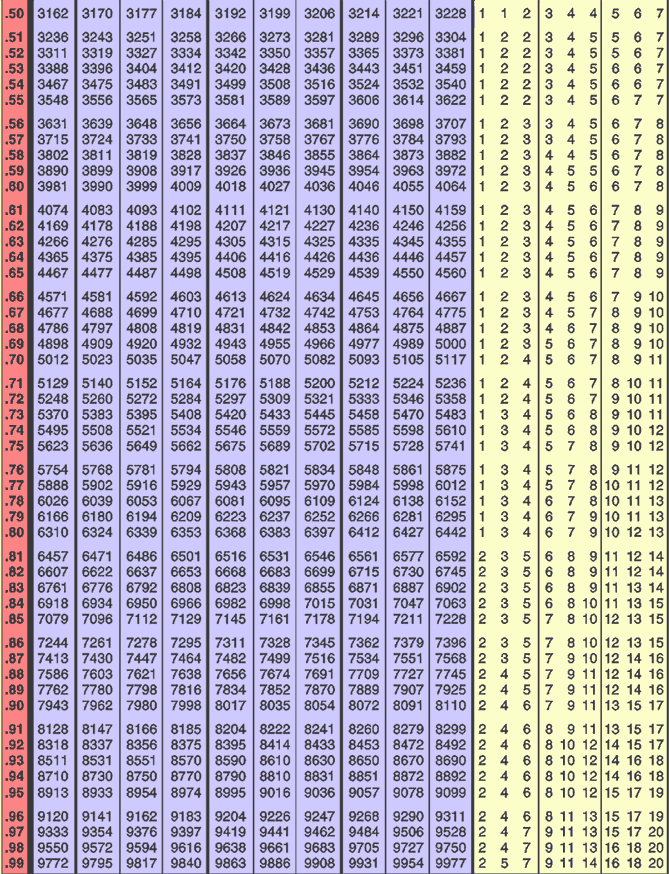
Example 2: Calculate the antilog of 2.7845

Given logarithm: 2.7845

Characteristic: 2

Mantissa: 0.7845

Find the value for the first three digits of the mantissa (0.784):

Locate row 0.78 and column 4 in the table.

The corresponding value is 6081.

How to Calculate Antilogarithms

Adjust for the fourth digit (5) using the mean difference:

In row 0.780, locate column 5 in the mean difference section.

The mean difference value is 7.

Add the base value and the mean difference:

6081+7 = 6081 + 2 = 6088

Insert the decimal point:

Add 1 to the characteristic (2+1=3).

Place the decimal after the third digit: 608.8

The antilog of 2.7845 is 608.8

How to Calculate Antilogarithms

Difference Between Antilogarithm and Logarithm Tables

Antilog and log tables are mathematical tools used to simplify complex calculations involving exponentials and logarithms. While both serve as reference tools for manual computations, they perform opposite operations and are used in different scenarios. Below is a detailed comparison of the two:

Difference Between Antilogarithm and Logarithm Tables
Aspect	Antilogarithm Table	Logarithm Table
Definition	A table is used to reverse a logarithmic value, helping retrieve the original number from its logarithm.	A table that provides the logarithmic value of a given number, typically to base 10 or base e.
Purpose	Converts logarithmic results back to their original form (inverse of logarithm).	Simplifies calculations by converting numbers into logarithmic scales.
Content	Lists numbers corresponding to exponential values derived from logarithms.	Contains the logarithmic values of numbers for commonly used bases like 10 or e.
Usage	Used to perform operations involving exponential calculations or reverse logarithms.	Used for simplifying multiplication, division, or handling very large or small values.
Example	If log⁡10(x)=0.301, the antilog table gives x=100.301≈2x	If x=100, the log table gives log⁡10(100)=2
Applications	Commonly applied in exponential growth, decay problems, and scientific data modeling.	Widely used in fields like engineering, mathematics, and science for dealing with orders of magnitude.

Antilog tables were once the go-to tool for solving tricky calculations involving logarithms and exponents, making seemingly impossible math manageable.

While modern technology has taken its place, learning about antilog tables is still fascinating. It connects us to a time when precision relied on skill, and understanding their use can sharpen your grasp of logarithmic and exponential calculations.

How to Calculate Antilogarithms

Read Also – Surface Area Formulas: Definitions, Derivations, Examples

Reference