Co Prime Numbers – Definition, Properties and Examples
Co prime numbers are pairs of numbers with no common divisors other than 1. Learn about co-primality, examples, and its importance in number theory and applications.
Co prime Numbers, also known as relatively prime numbers, are pairs of numbers that have no common factors other than 1. In other words, their greatest common divisor (GCD) is 1.
For example, 8 and 15 are co-prime because the only divisor they share is 1, even though 8 is divisible by 2 and 4, and 15 by 3 and 5.
Co prime Numbers do not need to be prime themselves. For instance, 14 and 15 are co-prime, despite 14 being divisible by 2 and 7, and 15 by 3 and 5.
The concept of co-primality is fundamental in number theory and has applications in areas like cryptography, fractions, and modular arithmetic.
What are Co Prime Numbers?
Co prime Numbers are pairs of numbers that share no common divisors except for 1. To form a set of Co prime Numbers, there must be at least two numbers.
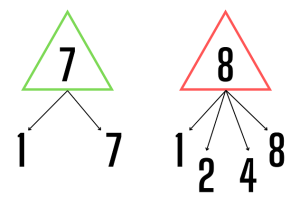
The highest common factor (HCF) of such numbers is always 1. For example, the numbers (4, 7) and (5, 9) are co-prime. It’s important to note that Co prime Numbers are not necessarily prime numbers themselves.
Even two composite numbers, like 4 and 9, can form a pair of co-primes. If the greatest common divisor (GCD) of two numbers, say a and b, is 1, then a and b are considered Co prime Numbers, and this pair is called a co-prime pair. Co prime Numbers are sometimes referred to as relatively prime numbers.
Properties of Co prime Numbers
Co prime Numbers can be easily identified through several key properties, which are outlined below:
The Highest Common Factor (HCF) of two Co prime Numbers is always 1. For instance, 5 and 9 are Co prime Numbers, so HCF(5, 9) = 1. The Least Common Multiple (LCM) of two Co prime Numbers is equal to their product. For example, since 5 and 9 are co-prime, LCM(5, 9) = 45. Additionally, the number 1 forms a co-prime pair with every integer.
It is important to note that two even numbers cannot be co-prime, as they will always share 2 as a common factor. Furthermore, the sum of two Co prime Numbers is co-prime with their product. For example, with 5 and 9 being co-prime, their sum, 5 + 9 = 14, is co-prime with their product, 5 × 9 = 45.
Moreover, any two prime numbers are always co-prime since they only share 1 as a common factor. For instance, 29 and 31 are both prime numbers, with their only common factor being 1. This property holds true for any pair of prime numbers, such as 2 and 3, 5 and 7, or 11 and 13.
Lastly, all pairs of consecutive numbers are co-prime. Any two consecutive integers will have 1 as their only common factor.
How to Find Co Prime Numbers?
Co prime Numbers (also known as relatively prime numbers) are pairs of numbers that have no common factor other than 1. This means the highest common factor (HCF) or greatest common divisor (GCD) of the numbers is 1.
- Check the HCF: To determine if two numbers are co-prime, you need to check their HCF. If the HCF is 1, the numbers are co-prime.
- Example:
- Consider the numbers 8 and 15.
- The factors of 8 are 1, 2, 4, 8.
- The factors of 15 are 1, 3, 5, 15.
- The only common factor between 8 and 15 is 1, so they are co-prime.
- Example:
- Using Prime Factorization:
- Another method to check if two numbers are co-prime is by breaking them down into their prime factors.
- If they don’t have any common prime factors, then they are co-prime.
- Example:
- Consider the numbers 14 and 25.
- The prime factorization of 14 is 2 × 7.
- The prime factorization of 25 is 5 × 5.
- Since they don’t share any common prime factors, 14 and 25 are co-prime.
- Using Euclidean Algorithm:
- The Euclidean algorithm is an efficient method to find the HCF of two numbers. If the result is 1, the numbers are co-prime.
- Example:
- For 18 and 35:
- Apply the Euclidean algorithm:
- 35 ÷ 18 = 1, remainder 17.
- 18 ÷ 17 = 1, remainder 1.
- 17 ÷ 1 = 17, remainder 0.
- Since the remainder is 1, the HCF is 1, so 18 and 35 are co-prime.
- General Rule:
- If two numbers are consecutive integers (e.g., 5 and 6, or 12 and 13), they are always co-prime.
- Example: 10 and 11 are co-prime because their HCF is 1.
- Co-prime Set:
- To check if a set of more than two numbers is co-prime, you can find the HCF of all the numbers in the set. If the HCF is 1, the set is co-prime.
- Example:
- Consider the numbers 5, 9, and 14.
- The HCF of 5, 9, and 14 is 1, so they are co-prime.
Co Prime Numbers and Twin Prime Numbers
Co prime Numbers (also known as relatively prime numbers) are pairs of numbers that have no common factor other than 1. This means the highest common factor (HCF) or greatest common divisor (GCD) of the numbers is 1.
- Check the HCF: To determine if two numbers are co-prime, you need to check their HCF. If the HCF is 1, the numbers are co-prime.
- Example:
- Consider the numbers 8 and 15.
- The factors of 8 are 1, 2, 4, 8.
- The factors of 15 are 1, 3, 5, 15.
- The only common factor between 8 and 15 is 1, so they are co-prime.
- Example:
- Using Prime Factorization:
- Another method to check if two numbers are co-prime is by breaking them down into their prime factors.
- If they don’t have any common prime factors, then they are co-prime.
- Example:
- Consider the numbers 14 and 25.
- The prime factorization of 14 is 2 × 7.
- The prime factorization of 25 is 5 × 5.
- Since they don’t share any common prime factors, 14 and 25 are co-prime.
- Using Euclidean Algorithm:
- The Euclidean algorithm is an efficient method to find the HCF of two numbers. If the result is 1, the numbers are co-prime.
- Example:
- For 18 and 35:
- Apply the Euclidean algorithm:
- 35 ÷ 18 = 1, remainder 17.
- 18 ÷ 17 = 1, remainder 1.
- 17 ÷ 1 = 17, remainder 0.
- Since the remainder is 1, the HCF is 1, so 18 and 35 are co-prime.
- General Rule:
- If two numbers are consecutive integers (e.g., 5 and 6, or 12 and 13), they are always co-prime.
- Example: 10 and 11 are co-prime because their HCF is 1.
- Co-prime Set:
- To check if a set of more than two numbers is co-prime, you can find the HCF of all the numbers in the set. If the HCF is 1, the set is co-prime.
- Example:
- Consider the numbers 5, 9, and 14.
- The HCF of 5, 9, and 14 is 1, so they are co-prime.
By following these steps, you can identify whether two or more numbers are co-prime. This concept is important in number theory, cryptography, and solving Diophantine equations.
Co prime Numbers and Twin Prime Numbers
Understanding Co prime Numbers and Twin Prime Numbers involves recognizing key differences and properties. Here’s a breakdown:
1. Co prime Numbers:
Co prime Numbers, also known as relatively prime numbers, are pairs of numbers that share no common divisors except 1. In other words, their greatest common divisor (GCD) is 1.
- Example:
- (8, 15) are co-prime because their only common factor is 1. The factors of 8 are 1, 2, 4, and 8, and the factors of 15 are 1, 3, 5, and 15. Since their GCD is 1, they are co-prime.
- Co prime Numbers can include both prime and composite numbers. For example, 9 and 16 are co-prime, even though both are composite numbers.
Key Properties of Co prime Numbers:
- Co prime Numbers do not have any common factor other than 1.
- Any two consecutive integers are always co-prime (e.g., 5 and 6).
- A number and 1 are always co-prime, as the GCD of 1 and any number is always 1.
2. Twin Prime Numbers:
Twin prime numbers are pairs of prime numbers that differ by exactly 2. They are a special subset of prime numbers that are close together.
- Example:
- (3, 5) is a twin prime pair because both are prime, and the difference between them is 2.
- (11, 13) is another twin prime pair because both numbers are prime, and the difference is 2.
Key Properties of Twin Prime Numbers:
- Both numbers in the pair are prime.
- The difference between the two numbers is exactly 2.
- Not all primes are twin primes. For instance, 5 and 7 are twin primes, but 7 and 11 are not (the difference is 4).
Comparison Between Co prime Numbers and Twin Prime Numbers:
- Co prime Numbers: These can be prime or composite numbers, and they have no common divisors except 1.
- Twin Prime Numbers: Both numbers in the pair must be prime, and they must differ by exactly 2.
Examples:
- Co-prime pairs:
- (8, 15), (9, 16), (14, 25)
- Twin prime pairs:
- (3, 5), (11, 13), (17, 19)
Co prime Numbers are any two numbers with no common factors other than 1, while twin prime numbers are specific pairs of prime numbers that are exactly two units apart.
While both concepts deal with prime numbers in some way, they are distinct from one another. Co prime Numbers can involve any type of number (prime or composite), while twin primes only involve prime numbers and must satisfy the condition of differing by exactly two.
Read More : Ratio: Meaning, Formulas, How to Solve, Types, Examples

My name is Khushi, I am a content writer and I provide news related to government jobs and I am from Rajasthan and I only write on this website.