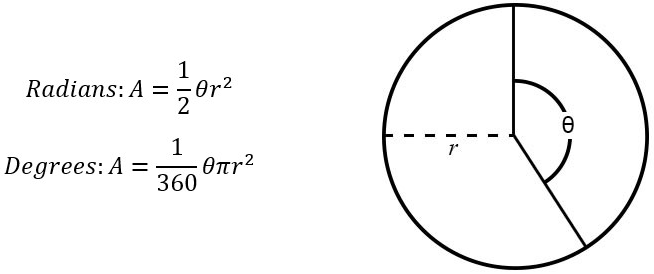Area of a Sector Circle Definition, Formula, Derivation, and Examples
Area of a Sector Circle is defined as the portion of a circle enclosed by two radii and an arc. Learn the steps to calculate the area of a sector with examples here.
The Area of a Sector Circle is the area of the pie-shaped portion of any circular shape we often encounter in day-to-day life. The concept of the sector and the calculation of its area have significant applications in mathematics, science, and engineering.
In this article, we will let you know about the sectors of a circle and the different ways to determine their area to help you understand and apply the concept comprehensively.
What is a Sector?
The Area of a Sector Circle is the portion of a circle formed by a part of the circumference (also known as an arc) and the two radii of the circle that touch the circle circumference at the two ends of the arc.
So, it is an area enclosed by an arc and two radii originating from the circle’s center. The angle between the two radii determines the size of the sector.
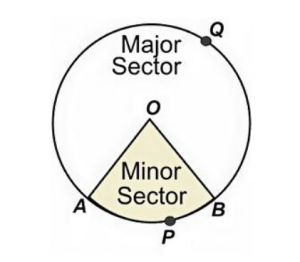
Minor and Major Sectors
The two radii in the circle always form two sectors, one smaller and the other larger. These are explained below.
Minor Sector: It is the smaller sector formed by the two radii when the angle between them is less than 180 degrees.
Major Sector: It is the larger sector formed by the two radii where the angle between them is more than 180 degrees.
In the above figure, two radii OA and OB from the center O touch the circle circumference at points A and B, forming two different sectors. The sector OAB is smaller and is called the minor sector. The OAQB sector is larger and is called the major sector. The angle AOB formed at the center determines the size of the sectors.
Area of Sector Circle
The Area of a Sector Circle is the space occupied by that particular portion or ’slice’ of the circle within the total boundary of the circle.
It is observed that the area of a sector depends on the angle created by the two radii at the center of the circle.
The size of the area increases with the increase in this angle. It means the area of a sector is directly proportional to the angle formed at the center of the circle.
Area of a Sector Circle Formula
The formula for sector area is based on the ratio of the angle formed at the center to the total angle. There can be two formulas for the sector of a circle, as mentioned below.
When the Angle is in Degrees
When θ is the angle at the center given in degrees and r is the radius of the circle, then the Area of sector = (θ/360) × πr2
When the Angle is in Radians
When θ is the angle at the center given in radians and r is the radius of the circle, then the Area of the sector = (θ/2π) × πr2 = ½θ x r2
Area of Sector Formula Derivation
The Area of a Sector Circle is derived using the following two concepts:
- The area of a circle is πr2 where r is the circle’s radius.
- The angle at the circle’s center, which encompasses the entire area, is 360 degrees.
Therefore, the area of a circle is πr2, which corresponds to the angle of 360 degrees.
Using the unitary method, we can say that if the two radii form an angle of 1 degree at the center of the circle, then the area of a sector formed will be πr2 /360.
Similarly, if the angle formed at the center of the circle is θ, the Area of the sector formed will be (θ/360) × πr2
Steps to Find Area of Sector Using Arc Length
The Area of a Sector Circle can be determined without knowing the angle formed at the center. In that case, we require the length of the arc corresponding to that sector for calculation purposes.
If the length of the arc is given as l and the radius of the circle is r, we can derive the formula for the sector as follows:
According to the radian definition, the angle at the center of the circle corresponding to a sector is the ratio of arc length to the radius of the circle. So in this case, if θ is the angle in radians, then θ = l/r
So, the area of sector A = ½θ x r2 = ½ (l/r) x r2 = (l x r) /2
Area of Sector Solved Examples
1. Find the Area of a Sector Circle with a 7 cm radius and a central angle of 60°.
Solution:
r = 7 cm, θ = 60°
Using the formula of area of sector = θ/360×πr2 , we get,
Area = 60/360 x 22/7 x (7)2 = 1/6 x 22 x 7 = 25.67 square cm.
2. Find the Area of a Sector Circle with a 4 cm radius and a central angle of π/4 radians.
Solution:
r = 3 cm, θ = π/4
So, the area of the sector = ½ x (4)2 x π/4 = (16/2) x π/4 = 2π = 6.28 square cm.
3. Find the areas of minor and major sectors formed by an angle of 120 degrees in a circle of radius 5 cm.
Solution:
The angle made by the sector is θ = 120°. It is a minor sector
So, the area of the minor sector = (120°/360°) × (22/7) × 52 = 1/3 × 22/7 × 25 = 26.17 square cm.
The angle for the major sector is 360°- 120° = 240°
So, the area of the major sector = (240°/360°) × (22/7) × 52 = 2/3 × 22/7 × 25 = 52.34 square cm.
4. The arc length of a sector is 10 cm, and the radius of the circle is 6 cm. Find the area of the sector.
Solution:
The arc length l = 10 and radius r = 6
Using the formula for the area of sector A = (l x r) /2, we get,
Area of sector = (10 x 6)/2 = 30 square cm.
The Area of a Sector Circle is an interesting mathematical concept that has various practical applications. An understanding of the Area of a Sector Circle for any circular shape gives a clear idea of how much portion of the total circle you are taking into consideration and how it is related to the angle created at the center of the circle.
Read More : Corresponding Angles: Definition, Theorem, and Solved Examples

My name is Khushi, I am a content writer and I provide news related to government jobs and I am from Rajasthan and I only write on this website.