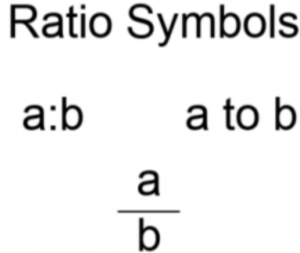Ratio: Meaning, Formulas, How to Solve, Types, Examples

Ratio: Meaning, Formulas, How to Solve, Types, Examples

A ratio is a mathematical expression that compares two or more quantities, showing the relative size of one quantity to another. It is often represented in the form of a fraction, with the first quantity (the numerator) divided by the second quantity (the denominator). Ratios can also be expressed using a colon (e.g., 3:2) or in words (e.g., “3 to 2”).

Ratios are commonly used in various fields, including mathematics, finance, and statistics, to analyze relationships between different values. For example, in finance, a company’s debt-to-equity ratio compares its total liabilities to its shareholders’ equity, providing insight into its financial leverage.

In everyday life, ratios can help compare prices, proportions in recipes, or the relationship between different measurements. Overall, ratios are a useful tool for understanding and interpreting relationships between quantities.

Ratio Formula

The formula for a ratio between two quantities, say ‘a’ and ‘b’, is expressed as:

a : b or a/b

This means that the ratio of ‘a’ to ‘b’ is the same as the fraction of ‘a’ over ‘b’.

To simplify the ratio, you divide both ‘a’ and ‘b’ by their greatest common divisor (GCD). For example, the ratio 6:9 can be simplified by dividing both numbers by 3, resulting in 2:3.

In general:

1. Step 1: Identify the two quantities (a and b).
2. Step 2: Divide both ‘a’ and ‘b’ by their greatest common divisor (GCD).
3. Step 3: Write the simplified ratio as a:b.

How to Solve Ratios?

Solving ratios can seem tricky at first, but with a clear process, you can tackle any ratio problem with confidence. Here’s a simple step-by-step guide to help you solve ratios effectively:

Step 1: Understand the Ratio

• Identify the Ratio: Look at the ratio you are given. For example, if you have a ratio of 3:4, this means for every 3 parts of one quantity, there are 4 parts of another quantity.
• Know What You Are Comparing: Determine what the two quantities represent. For example, if the ratio is of boys to girls in a class, you need to know how many boys and girls there are.

Step 2: Set Up the Equation

• Use Variables: If you need to find the actual quantities, you can use variables. For example, if the ratio of boys to girls is 3:4, you can let the number of boys be 3x and the number of girls be 4x, where x is a common multiplier.

Step 3: Write the Ratio as a Fraction

• Convert to Fraction: You can express the ratio as a fraction. For the ratio 3:4, you can write it as 3/4 This can help you when you need to solve for unknowns.

Step 4: Cross-Multiply (if necessary)

• Cross-Multiplication: If you are solving a proportion (where two ratios are equal), you can use cross-multiplication. For example, if you have 4:3​=12:x, you can cross-multiply:
  • ( 3times 12 = 4times x )
  • This gives you (36 = 4x).

Step 5: Solve for the Unknown

• Isolate the Variable: If you have an equation like ( 36 = 4x ), divide both sides by 4 to find x: (x = 36/{4} = 9).
• Find the Quantities: If you use variables in Step 2, substitute back to find the actual quantities. For example, if (x = 9), then:
  • Number of boys = ( 3x = 3 \times 9 = 27 )
  • Number of girls = ( 4x = 4 \times 9 = 36 )

Types of Ratios in Maths

Ratios are an important concept in math that helps us compare different quantities. Understanding ratios can make it easier to solve problems in various subjects, from math to science and even finance. Here’s a simple guide to the different types of ratios you might encounter:

1. Simple Ratios: These are the most straightforward type of ratio, comparing two quantities directly. For example, if you have 4 apples and 2 oranges, the ratio of apples to oranges is 4:2, which can be simplified to 2:1. This means for every 2 apples, there is 1 orange.
2. Compound Ratios: When you compare more than two quantities, you create a compound ratio. For instance, if a recipe calls for 2 cups of flour, 1 cup of sugar, and 3 eggs, the compound ratio is 2:1:3. This helps you understand the relationship between all the ingredients.
3. Proportional Ratios: These ratios show that two ratios are equal. For example, if the ratio of boys to girls in one class is 3:4 and in another class is 6:8, these ratios are proportional because they simplify to the same value (3:4). This means the relationship between boys and girls is the same in both classes.
4. Part-to-Whole Ratios: This type of ratio compares a part of a quantity to the whole. For example, if there are 20 students in a class and 8 of them are girls, the part-to-whole ratio of girls to the total number of students is 8:20, which simplifies to 2:5. This means that for every 5 students, 2 are girls.
5. Rate Ratios: These compare two quantities with different units. For example, if a car travels 120 miles in 2 hours, the rate ratio is 120 miles/2 hours, which simplifies to 60 miles per hour. This tells you how fast the car is going.

Examples

Imagine a classroom where the teacher counts the number of boys and girls. The teacher finds that the ratio of boys to girls is 4:5. If there are 20 boys in the classroom, how many girls are there?

Step 1: Understand it

The boys to girls is given as 4:5. This means that for every 4 boys, there are 5 girls.

Step 2: Set Up

Let’s denote:

• The number of boys = ( 4x )
• The number of girls = ( 5x )

Step 3: Use the Known Quantity

We know that there are 20 boys. So, we can set up the equation: [ 4x = 20 ]

Step 4: Solve for ( x )

To find ( x ), divide both sides of the equation by 4: [ x = \frac{20}{4} = 5 ]

Step 5: Find the Number of Girls

Now that we have ( x ), we can find the number of girls: [ \text{Number of girls} = 5x = 5 \times 5 = 25 ]

Step 6: Check the Ratio

Now, let’s check if the ratio of boys to girls is still 4:5:

• Number of boys = 20
• Number of girls = 25

Ratio of boys to girls = 20:25=4:5

Read More : Diagonal of Rectangle: Meaning, Properties, Formula, and Examples

Reference