Corresponding Angles: Definition, Theorem, and Solved Examples

Corresponding Angles: Definition, Theorem, and Solved Examples

Corresponding angles are equal angles formed when a transversal crosses parallel lines. Understand the corresponding angles theorem and its real-life applications here.

Corresponding Angle are an important fundamental concept in geometry that tells us the nature and relationship between angles when transversal lines intersect parallel lines.

As a math enthusiast or looking to apply this knowledge in real-world scenarios, understanding corresponding angles can enhance your knowledge of theoretical concepts and practical applications.

In this article, get useful insights into the concept of corresponding angles with detailed explanations and examples.

What are Corresponding Angles?

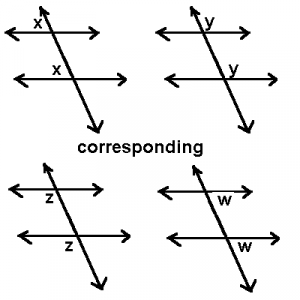
When two or more lines on the same plane are crossed by another line (called a transversal), the angles formed on the same side of the transversal are called corresponding angle. There can be two different instances of forming corresponding angles as follows:

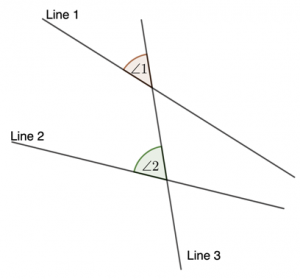
Angles formed by the intersection of non-parallel lines and a transversal

In the above figure, Line 1 and Line 2, which are not parallel to each other, are intersected by another Line 3, and the angles 1 and 2 formed are known as corresponding angles.

 

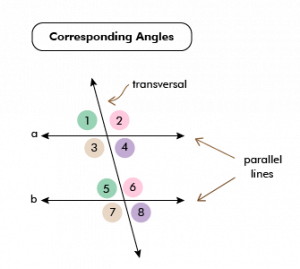
Angles formed by the intersection of parallel lines with a transversal

In the above image, the parallel lines l and m are crossed by a transversal, forming eight angles. In this case, the corresponding angles are denoted by:

Angles ∠1 and ∠5, because both angles are on the left-hand side of the transversal in the corresponding position.

Angles ∠2 and ∠6, because both angles are on the right-hand side of the transversal in the corresponding position.

Angles ∠3 and ∠7, because both angles are on the left-hand side of the transversal in the corresponding position.

Angles ∠4 and ∠8, because both angles are on the left-hand side of the transversal in the corresponding position.

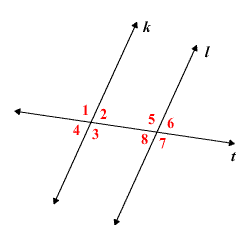
Interior and Exterior Angles

It is observed that there are always a pair of corresponding angle formed. Out of these two angles, one is called the interior angle, and the other is called the exterior angle.

In the above image, out of two corresponding angles ∠1 and ∠5, angle ∠1 is called the exterior angle because it is formed outside the parallel lines, and angle ∠5 is called the exterior angle as it is formed between the parallel lines.

Corresponding Angles Characteristics

There are particular characteristics or properties for the angle created when a transversal crosses parallel lines.

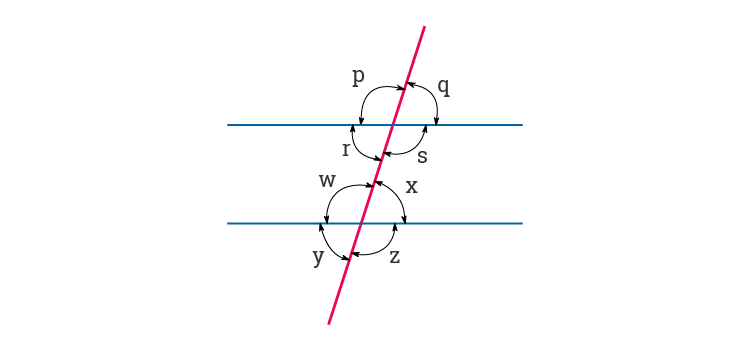
If two lines are parallel and a transversal line intersects them, then the measurement of corresponding angle formed on either side of the transversal are equal.

In the above figure, the two parallel lines are cut by a transversal. As a result, eight angles are formed between the lines and the transversal.

As per the theorem of corresponding angles, the angles formed by the first line with transversal and the corresponding angle formed by the second line with transversal are equal in measurement.

Therefore, we can say,

Angle ∠p = ∠w

Angle ∠q= ∠x

Angle ∠r = ∠y

Angle ∠s = ∠z

 

The Converse Theorem

The converse of the statement is also true. It means if a transversal intersects two lines in such a way that the corresponding angle formed are equal or congruent, then it can be said that the two lines are parallel to each other.

In the above image, we have found that four pairs of corresponding angles are formed between the transversal and two given lines and each angle of the pair is equal in measurement. Therefore, we can say that the lines are parallel.

Corresponding Angle of Polygons

Two polygons can be said to be similar when they are of the same shape but may be of different sizes. In such cases, their corresponding angle are congruent or equal.

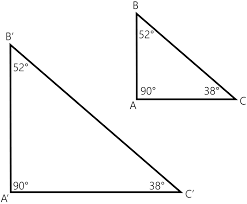
Let’s look at the following two similar triangles:

In these two triangles, angles A and Y are corresponding angles, angles C and Z are corresponding angles, and angles B and X are corresponding angles.

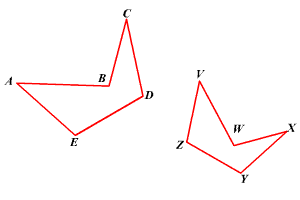
The same is true for the following two pentagons.

Here, the corresponding angle are equal, which means:

Angle ∠A = ∠V

Angle ∠B= ∠W

Angle ∠C = ∠X

Angle ∠D = ∠Y

Angle ∠E = ∠Z

Application of Corresponding Angles

Corresponding angle make many everyday tasks easier and more accurate. Here are a few real-life applications of corresponding angles:

• Building Bridges and Roads: Corresponding angle help make bridges and roads straight and safe by keeping parts in the right position.
• Designing Buildings: Architects use these angles to design walls, windows, and roofs to be perfectly aligned.
• Making Patterns: Artists use corresponding angle to create beautiful and even patterns in their work.
• Sports and Games: In sports like golf or archery, these angles help players aim better by measuring heights and slopes.
• Machines and Gears: Engineers use them to make sure parts of machines and gears fit together and work smoothly.
• Navigation: Pilots and sailors use corresponding angle to figure out directions and distances.

Corresponding Angles Solved Examples 

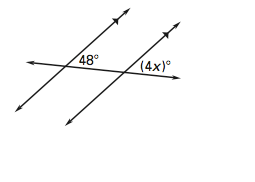
1. In the image given below, find the value of x

Solution:

Applying the theorem of corresponding angles, we can write:

4X = 48

Or, x = 48/4 = 12

Ans. The value of x is 12.

In the figure given below, find the value of x and y.

Solution:

Lines AB and CD are parallel which are intersected by a transversal. As per the properties of corresponding angles, we can write:

x =130

Again, using the corresponding angle and complementary angle theorem, we can say,

y + 50 = 180

Or, y = 150-80 = 130

Read More: Radius of a Circle: Definition, Formula, How to Find, and Examples

Reference